刷题笔记

发表于

从现在开始，按照leetcode专题刷题。此博文持续更新。

注意点：

  1. 写完函数，该return的记得return!
  2. 不要丢三落四！！！
    1. 树，不仅要会递归写法，同·时也要会迭代写法。

操作系统相关

leetcode 146. LRU缓存机制

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
class LRUCache {
public:
    // 千万记住，任何改动，都要看看hashmap和list用不用更新
    LRUCache(int capacity) {
        capacity_ = capacity;
    }
    
    int get(int key) {
        if (!hashmap.count(key)){
            return -1;
        }
        else {
            int value = hashmap[key]->second;
            lr.erase(hashmap[key]);
            lr.push_front({key, value});
            hashmap[key] = lr.begin();
            return value;
        }
    }
    void put(int key, int value) {
        if (hashmap.count(key)){
            // hashmap.erase(key);
            lr.erase(hashmap[key]);
        }
        else if (lr.size() >= capacity_){
            hashmap.erase(lr.back().first);
            lr.pop_back();
        }
        lr.push_front({key, value});
        hashmap[key] = lr.begin(); // 更新或添加
    }
private:
    int capacity_;
    list<pair<int, int>> lr;
    unordered_map<int, list<pair<int,int>>::iterator> hashmap;
};

/**
 * Your LRUCache object will be instantiated and called as such:
 * LRUCache* obj = new LRUCache(capacity);
 * int param_1 = obj->get(key);
 * obj->put(key,value);
 */

递归+回溯

汉诺塔

有三个柱子，分别为 from、buffer、to。需要将 from 上的圆盘全部移动到 to 上，并且要保证小圆盘始终在大圆盘上。

经典的递归问题，分为三步求解：

  1. 将n-1个圆盘从from -> buffer
  2. 将1个圆盘从from -> to
  3. 将n-1个圆盘从buffer->to
1
2
3
4
5
6
7
8
9
void move(int n, char from, char buffer, char to){
    if (n == 1){
        cout << "from" + from + "to" + to << endl;
        return;
    }
    move(n - 1, from, to, buffer);
    move(1, from, buffer, to);
    move(n - 1, buffer, from, to);
}

leetcode 46*. 全排列

老是记不住！！！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
vector<vector<int>> permute(vector<int>& nums) {
    vector<vector<int>> res;
    if (nums.size() == 0) return res;
    PermutationHelper(nums, 0, res);
    return res;
}
void PermutationHelper(vector<int> nums, int begin, vector<vector<int>>& res){
    if (begin == nums.size() - 1){
        res.push_back(nums);
        return;
    }
    for (int i = begin; i <= nums.size() - 1; i++){
        if (i != begin && nums[i] == nums[begin]){
            continue;
        }
        swap(nums[i], nums[begin]);
        PermutationHelper(nums, begin + 1, res);
        swap(nums[i], nums[begin]);
    }
}

leetcode 17. 电话号码的字母组合

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

img

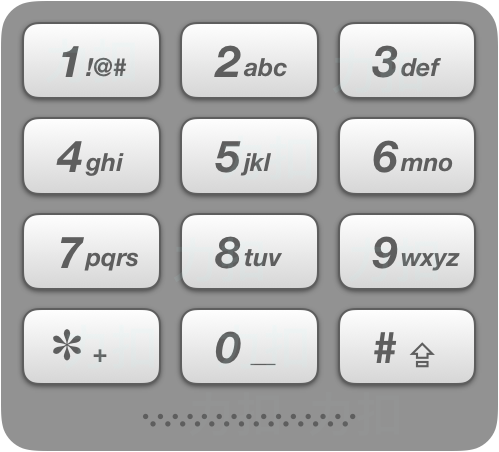
输入：“23”

输出：[“ad”, “ae”, “af”, “bd”, “be”, “bf”, “cd”, “ce”, “cf”].

思想：这道题和全排列有点像，也是用回溯。多记！！！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
vector<string> letterCombinations(string digits) {
    unordered_map<char, string> table{
        {'0', " "}, {'1',"*"}, {'2', "abc"},
        {'3',"def"}, {'4',"ghi"}, {'5',"jkl"},
        {'6',"mno"}, {'7',"pqrs"},{'8',"tuv"},
        {'9',"wxyz"}};  
    vector<string> res;
    if (digits == "") return res;
    helper(res, digits, "", table, 0);
    return res;
}
void helper(vector<string> &res, string digits, string str, unordered_map<char, string> m, int k){
    if (str.size() == digits.size()){
        res.push_back(str);
        return;
    }
    string temp = m[digits[k]];
    for (char x : temp){
        str += x;
        helper(res, digits, str, m, k+1);
        str.pop_back(); // 回溯
    }
    return;
}

leetcode 22. 括号生成

给出 n 代表生成括号的对数，请你写出一个函数，使其能够生成所有可能的并且有效的括号组合。

例如，给出 n = 3，生成结果为：

1
2
3
4
5
6
7
[
  "((()))",
  "(()())",
  "(())()",
  "()(())",
  "()()()"
]

貌似懂了一点点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
vector<string> generateParenthesis(int n) {
    vector<string> res;
    generate(res, "", 0, 0, n);
    return res;
}
void generate(vector<string>& res, string str, int l, int r, int n){
    if (l == n && r == n){
        res.push_back(str);
        return;
    }
    if (l > n || r > n || r > l) return;
    generate(res, str + '(', l + 1, r, n);
    generate(res, str + ')', l, r + 1, n);
}

链表

leetcode 19. 删除链表的倒数第N个节点

双指针。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
ListNode* removeNthFromEnd(ListNode* head, int n) {
    if (!head || !head->next) return NULL;
    ListNode* dummy = new ListNode(0);
    dummy->next = head;
    ListNode* fast = dummy, *slow = dummy;
    for (int i = 0; i < n + 1; i++){
        fast = fast->next;
    }
    while (fast){
        fast = fast->next;
        slow = slow->next;
    }
    ListNode *deleteNode = slow->next;
    slow->next = deleteNode->next;
    delete deleteNode;
    ListNode *newhead = dummy->next; // 有的情况下会把head删掉，所以要设置newhead！！！
    return newhead;
}

ListNode* removeNthFromEnd(ListNode* head, int n) {
	ListNode* fast = head, *slow = head;
    for (int i = 0; i < n; i++){
        if (fast->next)
            fast = fast->next;
        else return head->next;
    }
    while (fast->next){
        fast = fast->next;
        slow = slow->next;
    }
    slow->next = slow->next->next;
    return head;
}

leetcode 141. 环形链表

1
2
3
4
5
6
7
8
9
10
bool hasCycle(ListNode *head) {
    if (!head || !head->next) return false;
    ListNode* slow = head, *fast = head->next;
    while (slow != fast){
        if (!fast || !fast->next) return false;
        slow = slow->next;
        fast = fast->next->next;
    }
    return true;
}

leetcode 反转链表

有多种出题的形式，第一种，将整个链表进行反转：

1
2
3
4
5
6
ListNode* reverseList(ListNode* head){
    if (!head || !head->next) return head;
    ListNode* last = reverseList(head->next);
    head->next->next = head;
    return last;
}

第二种，反转链表的前n个元素(n <= 链表长度)，需要记录后驱节点：

1
2
3
4
5
6
7
8
9
10
11
12
13
ListNode *successor = NULL; // 后驱结点
ListNode* reverseN(ListNode* head, int n){
    if (n == 1){
        // 记录第n + 1个结点
        successor = head->next;
        return head;
    }
    ListNode *last = reverseN(head->next, n - 1);
    head->next->next = head;
    // 让反转之后的head节点和后面的节点连起来
    head->next = successor;
    return last;
}

第三种，反转链表的一部分：给一个索引区间[m,n]（索引从1开始），仅仅反转区间中的链表元素：

1
2
3
4
5
6
ListNode* reverseBetween(ListNode* head, int m, int n){
    // 如果m = 1，相当于反转前n个元素
    if (m == 1) return reverseN(head, n);
    head->next = reverseBetween(head->next, m - 1, n - 1);
    return head;
}

栈

leetcode 225. 用队列实现栈

只需要一个队列来模拟栈即可。要删除栈顶元素，可以用如下操作，即循环pop和push。获取top元素同理，但记得末尾要添加为temp。

1
2
3
4
5
6
7
8
9
10
> int pop() {
> 	for (int i = 0; i < q.size() - 1; i++){
>        	q.push(q.front());
>        	q.pop();
> 	}
> 	int temp = q.front();
> 	q.pop();
> 	return temp;
> }
>

数组

leetcode 1. 两数之和

给定一个整数数组 nums 和一个目标值 target，请你在该数组中找出和为目标值的那 两个 整数，并返回他们的数组下标。

O(n)的做法，利用一个map来存储对应的值和下标，贴代码：

1
2
3
4
5
6
7
8
9
10
map<int, int> hashmap;
for (int i = 0; i < nums.size(); i++){
    int tmp = target - nums[i];
    if (hashmap.count(tmp) > 0){
        res.push_back(i);
        res.push_back(hashmap[tmp]);
        break;
    }
    hashmap[nums[i]] = i;
}

leetcode 3*. 找无重复字符的最长子串

不会做，这里要运用滑动窗口求解。

1
2
3
4
5
6
7
8
9
10
11
map<char, int> M;
int i = 0, maxlen = 0;
for (int j = 0; j < s.size(); j++){
    if (M.count(s[j])){
        i = max(M[s[j]], i); 
// i是截至j，以j为最后一个元素的最长不重复子串的起始位置
// 即索引范围是[i,j]的子串是以索引j为最后一个元素的最长子串
    }
    maxlen = max(maxlen, j - i + 1);
    M[s[j]] = j + 1;
}

leetcode 11. 盛最多水的容器

思路只差一点就做对了，加油啊！！有时候不要想得太多，先按照一开始的思路写写看。思想有点类似动态规划。

给你 n 个非负整数 a1，a2，…，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

img

代码：

1
2
3
4
5
6
7
8
9
10
11
12
int maxArea(vector<int>& height) {
    if (height.size() == 2) return min(height[0], height[1]);
    int i = 0, j = height.size() - 1;
    int maxnum = 0, temp;
    while (i < height.size() && j >= 0) {
        temp = (j - i) * min(height[i], height[j]);
        maxnum = max(maxnum, temp);
        if (height[i] > height[j]) j--;
        else i++;
    }
    return maxnum;
}

leetcode 15*. 三数之和

给定一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c ，使得 a + b + c = 0 ？找出所有满足条件且不重复的三元组。

注意：答案中不可以包含重复的三元组。

双指针：类似于滑动窗口题，需要先进行排序，再利用滑动窗口求解。但注意，由于不允许重复，因此在左右指针更新的时候，需要特别留意！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        // 同样是滑动窗口题，需要排序后才可以
        vector<vector<int>> res;
        if (nums.size() < 3) return res;
        sort(nums.begin(), nums.end());
        int left, right;
        for (int i = 0; i < nums.size(); i++){
            if (nums[i] > 0) return res; // 已排序，但第一个数字大于0，则跳过
            if (i > 0 && nums[i] == nums[i - 1]) continue; // 遇到重复数字，跳过
            left = i + 1; 
            right = nums.size() - 1;
            while (left < right){
                if (nums[i] + nums[left] + nums[right] == 0){
                    res.push_back({nums[i], nums[left], nums[right]});
                    // 如果两个while不写，会导致重复结果
                    while (left < right && nums[left] == nums[left + 1])
                        left = left + 1;
                    while (left < right && nums[right] == nums[right - 1])
                        right = right - 1;
                    left += 1; // 这里还要继续更新，不然无法退出while
                    right -= 1;
                }
                else if (nums[i] + nums[left] + nums[right] > 0){
                    right -= 1;
                }
                else {
                    left += 1;
                }
            }
        }
        return res;
    }
};

leetcode 16. 最接近的三数之和

方法与leetcode 15基本相同，同样是排序+滑动窗口。

leetcode 18. 四数之和

方法参考leetcode 15. 先进行排序，随后，我们首先将题目转化为三数之和，计算出新的target，从而可以求解。注意，仍然需要避免重复元素！！在每个循环初始化的时候，都要想清楚为什么。

还是不太会，这道题。。。希望不会出吧！有时间再做一次。

leetcode 31*. 下一个排列

实现获取下一个排列的函数，算法需要将给定数字序列重新排列成字典序中下一个更大的排列。

如果不存在下一个更大的排列，则将数字重新排列成最小的排列（即升序排列）。

必须原地修改，只允许使用额外常数空间。

以下是一些例子，输入位于左侧列，其相应输出位于右侧列。
1,2,3 → 1,3,2
3,2,1 → 1,2,3
1,1,5 → 1,5,1

参考思路：

  1. 判断按照字典序有木有下一个，如果完全降序(包括等号)就没有下一个，则要找第一个
  2. 如何判断有没有下一个呢？只要存在a[i-1]<a[i]的升序结构，则有下一个（我们要从右往左找）
  3. 当发现a[i-1]<a[i]的结构，则从[i, ]中找到最接近a[i-1]又大于a[i-1]的数字，由于降序，从右往左遍历即可得到k
  4. 交换a[i-1]和k，再对[i, ]进行排序。排序只需要首尾不停交换即可，因为已经是降序。

参考例子：比如[0,5,4,3,2,1]，下一个是[1,0,2,3,4,5]

1
2
3
4
5
6
7
8
9
10
11
// 简洁版答案
void nextPermutation(vector<int>& nums) {
    int n = nums.size();
    int i = n - 2, j = n - 1;
    while (i >= 0 && nums[i + 1] <= nums[i]) i--;
    if (i >= 0) {
        while (nums[j] <= nums[i]) j--;
        swap(nums[i], nums[j]);
    }
    reverse(nums.begin() + i + 1, nums.end());
}

字符串

leetcode 5*. 最长回文子串

这道题，百看不会，所以还是要多做很多很多次。

给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。

我记的是O(n^2)的做法，即遍历对称轴来找回文串：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
public:
    string longestPalindrome(string s) {
        if (s.size() <= 1) return s;
        string ans = "";
        int maxlen = 0;
        // 回文子串为奇数的情况, s[i]为中心轴
        for (int i = 0; i < s.size(); i++){
            int j = 0;
            // while循环
            while (i - j >= 0 && i + j < s.size() && s[i - j] == s[i + j]){
                if (maxlen < 1 + 2 * j){
                    maxlen = 1 + 2 * j;
                    ans = s.substr(i - j, maxlen);
                }
                j += 1;
            }
        }
        // 回文子串为偶数的情况，s[i],s[i+1]为中心轴
        for (int i = 0; i < s.size(); i++){
            int j = 0;
            while (i - j >= 0 && i + j + 1 < s.size() && s[i - j] == s[i + j + 1]){
                if (maxlen < 2 + 2 * j){
                    maxlen = 2 + 2 * j;
                    ans = s.substr(i - j, maxlen);
                }
                j += 1;
            }
        }
        return ans;
    }
};

还有更好的思路，马拉车算法O(N)：https://blog.csdn.net/csdnnews/article/details/82920678

  1. 先对字符串进行预处理，两个字符之间加上特殊符号#；
  2. 然后遍历整个字符串，用一个数组来记录以该字符为中心的回文长度，为了方便计算右边界，我在数组中记录长度的一半（向下取整）；
  3. 每一次遍历的时候，如果该字符在已知回文串最右边界的覆盖下，那么就计算其相对最右边界回文串中心对称的位置，得出已知回文串的长度；
  4. 判断该长度和右边界，如果达到了右边界，那么需要进行中心扩展探索。当然，如果第3步该字符没有在最右边界的“羽翼”下，则直接进行中心扩展探索。进行中心扩展探索的时候，同时又更新右边界；
  5. 最后得到最长回文之后，去掉其中的特殊符号即可。

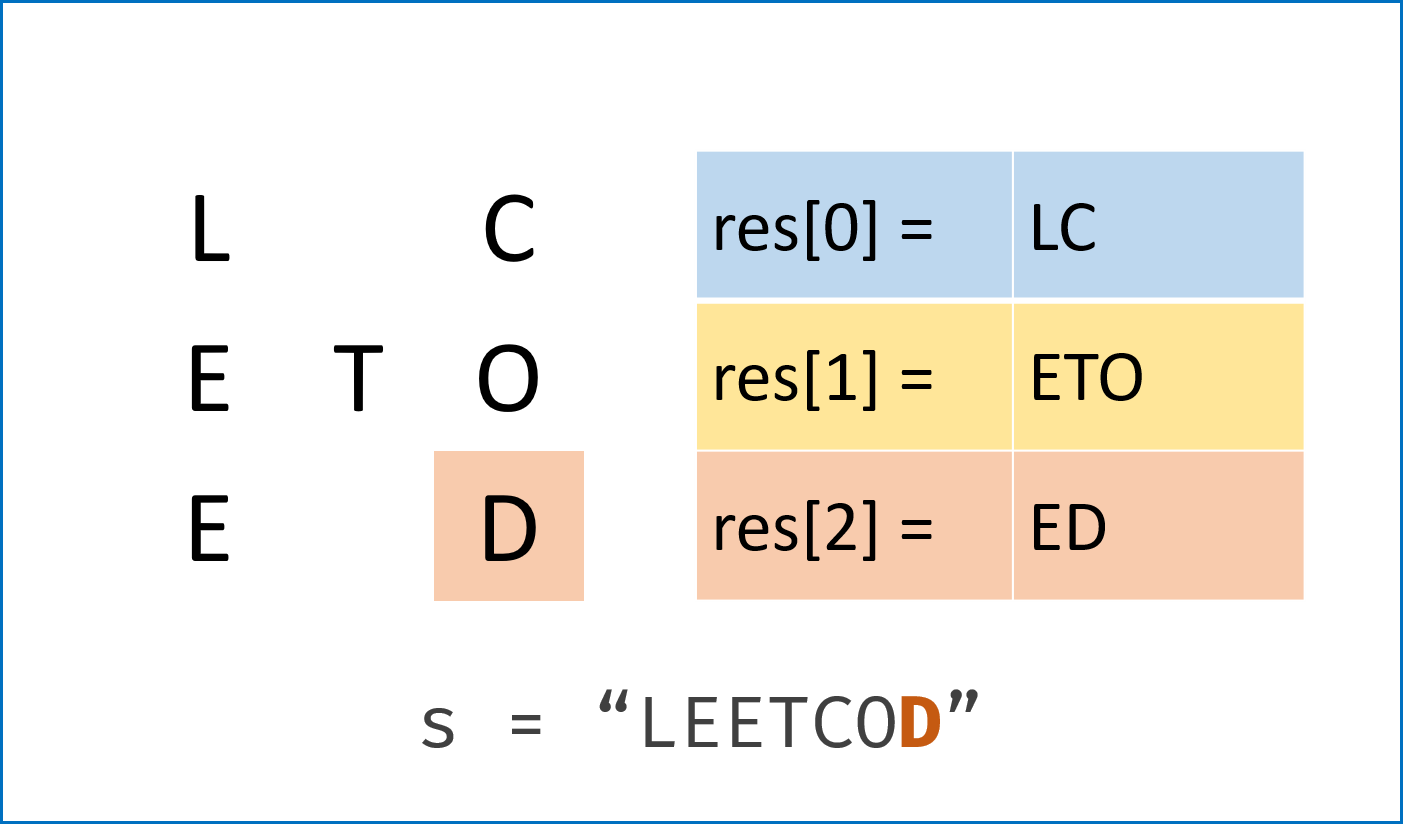
leetcode 6*. Z字形变换

将一个给定字符串根据给定的行数，以从上往下、从左到右进行 Z 字形排列。

比如输入字符串为 “LEETCODEISHIRING” 行数为 3 时，排列如下：

L C I R
E T O E S I I G
E D H N

巧妙的思想，用一维数组就可以得到结果，图示如下：

img

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
string convert(string s, int numRows) {
    string res[numRows];
    if (s.empty() || numRows < 1) return s;
    if (numRows == 1) return s;
    int i = 0, flag = -1; // 利用flag来改变存储方向
    for (int j = 0; j < s.size(); j++){
        res[i] += s[j];
        if (i == 0 || i == numRows - 1)
            flag = - flag;
        i += flag;
    }
    string ans;
    for (auto r : res){
        ans += r;
    }
    return ans;
}

leetcode 8. 字符串转换整数(atoi)

请你来实现一个 atoi 函数，使其能将字符串转换成整数。

首先，该函数会根据需要丢弃无用的开头空格字符，直到寻找到第一个非空格的字符为止。

当我们寻找到的第一个非空字符为正或者负号时，则将该符号与之后面尽可能多的连续数字组合起来，作为该整数的正负号；假如第一个非空字符是数字，则直接将其与之后连续的数字字符组合起来，形成整数。

该字符串除了有效的整数部分之后也可能会存在多余的字符，这些字符可以被忽略，它们对于函数不应该造成影响。

注意：假如该字符串中的第一个非空格字符不是一个有效整数字符、字符串为空或字符串仅包含空白字符时，则你的函数不需要进行转换。

在任何情况下，若函数不能进行有效的转换时，请返回 0。

说明：

假设我们的环境只能存储 32 位大小的有符号整数，那么其数值范围为 [−231, 231 − 1]。如果数值超过这个范围，请返回 INT_MAX (231 − 1) 或 INT_MIN (−231) 。

示例 1:

输入: “42”
输出: 42

示例 2:

输入: “ -42”
输出: -42
解释: 第一个非空白字符为 ‘-‘, 它是一个负号。
我们尽可能将负号与后面所有连续出现的数字组合起来，最后得到 -42 。

示例 3:

输入: “4193 with words”
输出: 4193
解释: 转换截止于数字 ‘3’ ，因为它的下一个字符不为数字。

示例 4:

输入: “words and 987”
输出: 0
解释: 第一个非空字符是 ‘w’, 但它不是数字或正、负号。
因此无法执行有效的转换。

示例 5:

输入: “-91283472332”
输出: -2147483648
解释: 数字 “-91283472332” 超过 32 位有符号整数范围。
因此返回 INT_MIN (−231) 。

这个问题其实没有过多的技巧，考察的是细心和耐心，并且需要不断地调试。在这里我简单罗列几个要点。

Java 、Python 和 C++ 字符串的设计都是不可变的，即使用 trim() 会产生新的变量，因此我们尽量不使用库函数，使用一个变量 index 去做线性遍历，这样遍历完成以后就得到转换以后的数值。

  • 根据示例 1，需要去掉前导空格；
  • 根据示例 2，需要判断第 1 个字符为 + 和 - 的情况，因此，可以设计一个变量 sign，初始化的时候为 1，如果遇到 - ，将 sign 修正为 -1；
  • 判断是否是数字，可以使用字符的 ASCII 码数值进行比较，即 0 <= c <= ‘9’；
  • 根据示例 3 和示例 4 ，在遇到第 1 个不是数字的字符的情况下，就得退出循环；
  • 根据示例 5，如果转换以后的数字超过了 int 类型的范围，需要截取。这里需要将结果 res 变量设计为 long 类型，注意：由于输入的字符串转换以后也有可能超过 long 类型，因此需要在循环内部就判断是否越界，只要越界就退出循环，这样也可以减少不必要的计算；
  • 因为涉及下标访问，因此全程需要考虑数组下标是否越界的情况。
    特别注意：由于题目中说“环境只能保存 32 位整数”，因此这里在每一轮循环之前先要检查乘以 1010 以后是否溢出，具体细节请见编码.

这里贴一下判断函数：

1
2
3
4
5
6
7
8
if (res > INT_MAX / 10 || (res == INT_MAX / 10 && (currChar - '0') > INT_MAX % 10)){
    // INT_MAX % 10 = 7
    return INT_MAX;
}
if (res < INT_MIN / 10 || (res == INT_MIN / 10 && (currChar - '0') > - (INT_MIN % 10))){
    //  -(INT_MIN % 10) = 8
    return INT_MIN;
}

leetcode 10*. 正则表达式匹配（困难）

1
2
3
4
5
6
7
8
9
10
11
bool isMatch(string s, string p) {
    if (p == ".*") return 1;
    if (p.empty()) return s.empty();
    auto first_match = !s.empty() && (s[0] == p[0] || p[0] == '.');
    if (p.length() >= 2 && p[1] == '*') {
        return isMatch(s, p.substr(2)) || (first_match && isMatch(s.substr(1), p));
    }
    else {
        return first_match && isMatch(s.substr(1), p.substr(1));
    }
}

leetcode 12. 整数转罗马数字

使用两个数组，存储对应的string和代表的数字。虽然再对num进行转换即可。

leetcode 13. 罗马数字转整数

使用字典存储罗马数字对应的数字。遍历字符串，如果当前的字符比右边的字符所代表的数字小，则减去当前字符所代表的数字；否则直接加上。也就是说，一个字符一个字符的处理，而不要想着按照string的方式来找准数字。

leetcode 14. 最长公共前缀

我的做法：先求出所有字符串中的最短长度，再遍历字符串来判断。时间复杂度相当于：字符串总数 * 最短字符串长度。

用python的话很简单诶，复杂度只有O(N)，求出最短的和最长的两个字符串，再比较他们的最长公共前缀即可。

动态规划

我的弱点之一。

leetcode 10*. 正则表达式匹配

给你一个字符串 s 和一个字符规律 p，请你来实现一个支持 '.' 和 '*' 的正则表达式匹配。

1
2
3
> '.' 匹配任意单个字符
> '*' 匹配零个或多个前面的那一个元素
>

递归

1
2
3
4
5
6
7
8
9
10
11
bool isMatch(string s, string p) {
    if (p == ".*") return 1;
    if (p.empty()) return s.empty();
    auto first_match = !s.empty() && (s[0] == p[0] || p[0] == '.');
    if (p.length() >= 2 && p[1] == '*') {
        return isMatch(s, p.substr(2)) || (first_match && isMatch(s.substr(1), p)); // 前者是直接跳过，不匹配；后者是匹配一个
    }
    else {
        return first_match && isMatch(s.substr(1), p.substr(1));
    }
}

leetcode 53. 最大子序和

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

示例:

输入: [-2,1,-3,4,-1,2,1,-5,4],
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。

首先，来理解最标准的动态规划做法。

初始化一个dp数组，用来存储当前数组位置所对应的最大和。其中，初始状态为dp[0] = nums[0]。状态转移方程为：dp[i] = max(0, dp[i-1]) + nums[i]。

1
2
3
4
5
6
7
8
9
10
int maxSubArray(vector<int>& nums) {
    vector<int> dp(nums.size());
    dp[0] = nums[0];
    int sum = nums[0];
    // dp[i] = max(dp[i - 1], 0) + nums[i] 状态转移方程
    for (int i = 1; i < nums.size(); i++){
        dp[i] = max(dp[i - 1], 0) + nums[i];
        sum = max(sum, dp[i]);
    }
}

从状态转移方程可以看到，dp[i] = max(dp[i - 1], 0) + nums[i]看出，当前状态的值只取决于前一个状态值，所以我们可以用一个变量来代替dp[i-1]：

1
2
3
4
5
6
7
8
9
int maxSubArray(vector<int>& nums) {
    int temp = nums[0];
    int sum = nums[0];
    for (int i = 1; i < nums.size(); i++){
        temp = max(temp, 0) + nums[i];
        sum = max(temp, sum);
    }
    return sum;
}

leetcode 62. 不同路径

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

问总共有多少条不同的路径？

使用二维数组作为状态方程，表示到达该位置的路径数。其中，初始状态，第一行和第一列的值为1。接着需要设计状态转移方程，其实通过观察也可以发现：dp[i][j] = dp[i-1][j] + dp[i][j-1]。（要努力培养这种思维，即如何利用之前已经获得的值呢？）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int uniquePaths(int m, int n) {
    int dp[100][100];
    for (int i = 0; i < m; i++){ //状态初始化
        dp[i][0] = 1;
    }
    for (int i = 0; i < n; i++){ //状态初始化
        dp[0][i] = 1;
    }
    for (int i = 1; i < m; i++){
        for (int j = 1; j < n; j++){
            dp[i][j] = dp[i-1][j] + dp[i][j-1];
        }
    }
    return dp[m-1][n-1];
}

leetcode 63*. 不同路径II

同样使用动态规划来做，做法和62基本相同。不同之处在于，多了障碍物，所以初始化的时候需要注意：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int flag = 0;
for (int i = 0; i < obstacleGrid.size(); i++){ // 对第一列进行初始化
    if (obstacleGrid[i][0] == 1){ // 存在障碍物
        flag = 1;
    }
    if (flag == 0) dp[i][0] = 1;
    else dp[i][0] = 0;
}
flag = 0;
for (int i = 0; i < obstacleGrid[0].size(); i++){ // 对第一行进行初始化
    if (obstacleGrid[0][i] == 1){ // 存在障碍物
        flag = 1;
    } 
    if (flag == 0) dp[0][i] = 1;
    else dp[0][i] = 0;
}

状态转移方程和之前一致。另外要注意，如果我们的dp数组用int来存值，那么在中间会有计算结果超过int值表示。因此要修改成dp数组改成long表示。

另外，用vector初始化二维数组：

1
vector<vector<int>> v(rows, vector<int>(cols, 0));

leetcode 64. 最小路径和

还是比较简单的。我使用二维数组来做dp数组，状态转移方程为：

1
dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j];

leetcode 70. 爬楼梯

其实是斐波那契数列题，也可以用动态规划的思想来理解。91题的思想要从这道题参考。

leetcode 91*. 解码方法

一条包含字母 A-Z 的消息通过以下方式进行了编码：

‘A’ -> 1
‘B’ -> 2
…
‘Z’ -> 26
给定一个只包含数字的非空字符串，请计算解码方法的总数。

示例 1:

1
2
3
4
> 输入: "12"
> 输出: 2
> 解释: 它可以解码为 "AB"（1 2）或者 "L"（12）。
>

>

示例 2:

1
2
3
4
> 输入: "226"
> 输出: 3
> 解释: 它可以解码为 "BZ" (2 26), "VF" (22 6), 或者 "BBF" (2 2 6) 。
>

这一题，我做了很多次，但是都是错的。原因有两个：

  1. 将动态规划的思想给搞错了，没有体会题目的含义；
  2. 没有注意到0这个边界条件的额外处理。

正确的思路是这样的：

  1. 我们知道最后一个字母有可能是由一个数字串或两个数字串转化而来，例如’12312’这个数字串，转化成字母串最后一位可以是’2’转成B，也可能是’12’转成L。

  2. 这就有点类似跳台阶问题。设数字串S的前i个数字解密成字母串有dp[i]种方式：那么就有dp[i] = dp[i-1] + dp[i-2]。

    dp[i-1]表示最后一个数字解码成一个字母；

    dp[i-2]表示最后两个数字解码成一个字母。

而我的错误，就是没有看清楚本质，而是一直在处理各种边界条件的情况下死磕着，这是非常错误的！！通常情况下，状态转移方程不会有过多复杂的情况（正则表达式那一题除外）。因此，要自己认真体会！！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// dp[i + 1] = dp[i] + dp[i - 1];
int numDecodings(string s) {
    if (s.size() == 0 || (s.size() == 1 && s[0] == '0')) return 0;
    if (s.size() == 1) return 1;
    vector<int> dp(s.size() + 1, 0);
    dp[0] = 1;
    for (int i = 0; i < s.size(); i++){
        dp[i + 1] = s[i] == '0' ? 0 : dp[i]; 
        // 如果为0，则表示这一位数字不能解码为一个字母，因此加0
        if (i > 0 && (s[i-1] == '1' || (s[i-1] == '2' && s[i] <= '6'))){
            dp[i + 1] += dp[i - 1];
        }
    }
    return dp.back();
}

leetcode 96*. 不同的二叉搜索树

要知道怎么找规律。我们设$G(n)$代表n个整数为节点构成的二叉搜索树个数。其中，令$f(i)$表示第i个结点为根的二叉搜索树个数，则有：

而$f(i)$又可以表示为以i为根节点，再结合左右子树的值：

因此有：

贴贴代码：

1
2
3
4
5
6
7
8
9
10
11
int numTrees(int n) {
    if (n == 1) return 1;
    vector<int> dp(n + 1, 0);
    dp[0] = 1;
    for (int i = 1; i <= n; i++){
        for (int j = 0; j < i; j++){
            dp[i] += dp[j] * dp[i - j - 1];
        }
    }
    return dp[n];
}

leetcode 120. 三角形最小路径和

给定一个三角形，找出自顶向下的最小路径和。每一步只能移动到下一行中相邻的结点上。例如，给定三角形：

1
2
3
4
5
6
[
     [2],
    [3,4],
   [6,5,7],
  [4,1,8,3]
]

自顶向下的最小路径和为 11（即，2 + 3 + 5 + 1 = 11）。

思路：使用二维dp数组，先初始化后，根据状态转移方程进行更新。

1
2
3
4
5
6
7
8
9
if (j == 0) { // 第0列
    dp[i][j] = dp[i-1][j] + triangle[i][j];
}
else if (j == i){
    dp[i][j] = dp[i-1][j-1] + triangle[i][j];
}
else {
    dp[i][j] = min(dp[i-1][j-1], dp[i-1][j]) + triangle[i][j];
}

之后，再找最后一行的最小值即可。另外，上述代码是自顶向下求；而自底向上求会更加方便，因为dp[i][j] = min(dp[i+1][j], dp[i+1][j+1]) + triangle[i][j]必成立，不需要额外判断。另外，还可以在原输入的基础上修改，做到空间复杂度为O(1)。

贴代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// 一维dp数组
if (triangle.size() == 0) return 0;
vector<int> dp(triangle.size() + 1, 0); // dp中记录了求第i行时，第i+1行的最小路径和
for (int i = triangle.size() - 1; i >= 0; i--){
    for (int j = 0; j < triangle[i].size(); j++){
        dp[j] = min(dp[j+1], dp[j]) + triangle[i][j];
    }
}
return dp[0];

// 原数组修改
for (int i = triangle.size() - 2; i >= 0; i--){
    for (int j = 0; j < triangle[i].size(); j++){
        triangle[i][j] += min(triangle[i+1][j], triangle[i+1][j+1]);
    }
}
return triangle[0][0];

leetcode 312*. 戳气球（困难）

有 n 个气球，编号为0 到 n-1，每个气球上都标有一个数字，这些数字存在数组 nums 中。

现在要求你戳破所有的气球。每当你戳破一个气球 i 时，你可以获得 nums[left] nums[i] nums[right] 个硬币。 这里的 left 和 right 代表和 i 相邻的两个气球的序号。注意当你戳破了气球 i 后，气球 left 和气球 right 就变成了相邻的气球。

求所能获得硬币的最大数量。

说明:

  • 你可以假设 nums[-1] = nums[n] = 1，但注意它们不是真实存在的所以并不能被戳破。
  • 0 ≤ n ≤ 500, 0 ≤ nums[i] ≤ 100

示例:

输入: [3,1,5,8]
输出: 167
解释: nums = [3,1,5,8] —> [3,5,8] —> [3,8] —> [8] —> []
coins = 315 + 358 + 138 + 181 = 167

记录一道困难的动态规划题，貌似网易很喜欢出。

动态规划：

经过一连串的分析（其实我看不太懂这个分析）https://qoogle.top/leetcode-312-burst-balloons/ 总之，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
vector<vector<int>> dp;
int maxCoins(vector<int>& nums) {
    int n = nums.size();
    nums.insert(nums.begin(), 1);
    nums.push_back(1);
    dp = vector<vector<int>> (n + 2, vector<int>(n + 2, 0));
    int ans = helper(nums, 1, n);
    return ans;
}
int helper(vector<int>& nums, int i, int j){ 
    // 问题区间，从第i到第j个气球，能获得的最大硬币数量
    // 边界
    if (i > j) return 0;
    if (dp[i][j] > 0) return dp[i][j];
    // 查找
    for (int k = i; k <= j; k++){
        int left = helper(nums, i, k - 1);
        int right = helper(nums, k + 1, j);
        // 因为第k个气球是最后引爆的，所以其相邻气球应该是区间的左右两端
        int delta = nums[k] * nums[i - 1] * nums[j + 1];
        dp[i][j] = max(dp[i][j], left + right + delta);
        // dp[i][j]表示从i到j个气球（闭区间）能够获取的最大的硬币数量
    }
    return dp[i][j];
}

322. 零钱兑换

给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1。

示例1：

1
2
3
输入：coins = [1,2,5], amount = 11
输出：3
解释：11 = 5 + 5 + 1

思想：我总想着怎么用贪心来解，殊不知，这是一道动态规划题。。。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int coinChange(vector<int>& coins, int amount) {
    // 动态规划 - 完全背包问题
    // dp[i] = (\min_{j=0,...,n - 1} dp[i - cj]) + 1
    // 其中,cj表示硬币的金额数
    vector<int> dp(amount + 1, 0);
    dp[0] = 0;
    for (int i = 1; i <= amount; i++){
        int temp = INT_MAX - 1;
        for (int j = 0; j < coins.size(); j++){
            if (i - coins[j] < 0) continue;
            if (temp > dp[i - coins[j]]) temp = dp[i - coins[j]];
        }
        dp[i] = temp + 1;
    }
    return dp[amount] == INT_MAX ? -1 : dp[amount];
}

leetcode 121. 买卖股票的最佳时机

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。

如果你最多只允许完成一笔交易（即买入和卖出一支股票），设计一个算法来计算你所能获取的最大利润。

注意你不能在买入股票前卖出股票。

示例1：

1
2
3
4
输入: [7,1,5,3,6,4]
输出: 5
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
     注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格。

思路：动态规划。如果直接计算最大差值的话应该会超时。机灵一点！！！

1
2
3
4
5
6
7
8
9
10
11
12
int maxProfit(vector<int>& prices) {
    if (prices.size() <= 1) return 0;
    // 前i天的最大收益 = max{前i-1天的最大收益，第i天的价格-前i-1天中的最小价格}
    vector<int> dp(prices.size(), 0);
    dp[0] = -prices[0];
    int minp = prices[0];
    for (int i = 1; i < prices.size(); i++){
        dp[i] = max(dp[i - 1], prices[i] - minp);
        if (minp > prices[i]) minp = prices[i];
    }
    return dp[prices.size() - 1] > 0 ? dp[prices.size() - 1] : 0;
}

122. 买卖股票的最佳时机II

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易（多次买卖一支股票）。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例1：

1
2
3
4
输入: [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
     随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。

一直在想着要怎么用动态规划，万万没想到，这道题却是脑筋急转弯。。。

1
[7, 1, 5, 6] 第二天买入，第四天卖出，收益最大（6-1），所以一般人可能会想，怎么判断不是第三天就卖出了呢? 这里就把问题复杂化了，根据题目的意思，当天卖出以后，当天还可以买入，所以其实可以第三天卖出，第三天买入，第四天又卖出（（5-1）+ （6-5） == 6 - 1）。所以算法可以直接简化为只要今天比昨天大，就卖出。
1
2
3
4
5
6
7
8
9
int maxProfit(vector<int>& prices){
    int cnt = 0;
    for (int i = 1; i < prices.size(); i++){
        if (prices[i] > prices[i - 1]){
            cnt += prices[i] - prices[i - 1];
        }
    }
    return cnt;
}

链表

leetcode 206. 反转链表

今天，一直不擅长的题目做出来了！（也可能是因为之前做过）我的体会是，可以用画图的方式来看答案，就是自己摸清楚需要记录什么结点，结点之间的关系怎么变换，应该就可以懂了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
// 迭代做法
ListNode* reverseList(ListNode* head){
    if (!head) return NULL;
    ListNode *pre = NULL, *pro;
    ListNode *ReverseHead;
    while (head){
        pro = head->next;
        head->next = pre;
        if (pro == NULL){
            ReverseHead = head;
            break;
        }
        pre = head;
        head = pro;
    }
    return ReverseHead;
}
 
// 递归做法
ListNode* reverseList(ListNode* head){
    if (!head || !head->next) return head;
    ListNode *newhead = reverseList(head->next);
    head->next->next = head;
    head->next = NULL;
    return newhead;
}

leetcode 203 删除链表中等于给定值val的所有节点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
ListNode* removeElements(ListNode* head, int val) {
    if (!head) return NULL;
    ListNode* newhead = new ListNode(0);
    newhead->next = head;
    ListNode* pre = newhead, *p = head;
    while (p){
        if (p->val == val){
            pre->next = p->next;
        }
        else {
            pre = p;
        }
        p = p->next;
    }
    return newhead->next;
}

二叉树

二叉树的题，都直接重新刷一遍。

leetcode 112. 路径总和

给定一个二叉树和一个目标和，判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和。

1
2
3
4
5
6
7
8
9
bool hasPathSum(TreeNode* root, int sum) {
    // base case考虑边界情况
    if (!root) return false;
    if (!root->left && !root->right){
        return sum - root->val == 0;
    }
    return hasPathSum(root->left, sum - root->val) ||
        hasPathSum(root->right, sum - root->val);
}

leetcode 94*. 二叉树的中序遍历

递归做法：

1
2
3
4
5
6
7
8
vector<int> res;
vector<int> inorderTraversal(TreeNode* root) {
    if (!root) return res;
    inorderTraversal(root->left);
    if (root) res.push_back(root->val);
    inorderTraversal(root->right);
    return res;
}

非递归，利用栈来做。看看代码就会理解！！！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
vector<int> inorderTraversal(TreeNode* root) {
    vector<int> res;
    stack<TreeNode*> S;
    while (root || !S.empty()){
        while (root){
            S.push(root);
            root = root->left;
        }
        if (!S.empty()) {
            root = S.top();
            S.pop();
            res.push_back(root->val);
            root = root->right;
        }
    }
    return res;
}

补充：前序遍历非递归写法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
vector<int> preorderTraversal(TreeNode* root) {
    vector<int> res;
    stack<TreeNode*> S;
    TreeNode* p = root;
    while (p || !S.empty()) {
        while (p) {
            res.push_back(p->val);
            S.push(p);
            p = p->left;
        }
        if (!S.empty()) {
            p = S.top();
            S.pop();
            p = p->right;
        }
    }
    return res;
}

与中序遍历非递归的不同点，在于访问结点的位置不同。前序遍历是在入栈时就访问，中序遍历是在出栈时访问。

补充：后序遍历非递归写法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
vector<int> postorderTraversal(TreeNode* root) {
    vector<int> res;
    if (!root) return res;
    TreeNode* p = root;
    stack<TreeNode*> S;
    TreeNode* temp;
    while (p || !s.empty()) {
        if (p) {
            S.push(p);
            p = p->left;
        }
        else {
            p = S.top();
            if (p->right && p->right != r) {
                p = p->right;
            }
            else {
                S.pop();
                res.push_back(p->val);
                r = p; //记录最近访问过的节点
                p = NULL; //重置
            }
        }
    }
}

leetcode 95*. 不同的二叉搜索树II

不太会，看答案。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
vector<TreeNode*> generateTrees(int n) {
    if (n) return generate(1, n);
    else return vector<TreeNode*>{};
}
vector<TreeNode*> generate(int left, int right){
    vector<TreeNode*> res;
    if (left > right){
        res.push_back(NULL);
        return res;
    }
    for (int i = left; i <= right; i++){
        vector<TreeNode*> left_nodes = generate(left, i - 1);
        vector<TreeNode*> right_nodes = generate(i + 1, right);
        for (TreeNode* left_node : left_nodes){
            for (TreeNode* right_node : right_nodes){
                TreeNode* r = new TreeNode(i);
                r->left = left_node;
                r->right = right_node;
                res.push_back(r);
            }
        }
    }
    return res;
}

leetcode 98. 验证二叉搜索树

有两个地方要注意：

  1. 不能出现相等的数字！
  2. 空节点也返回true，算是二叉搜索树。

第一种方法是通过中序遍历把结果保存到vector中，再依次判断；第二种方法是空间复杂度为O(1)，即边中序遍历边判断。但是，有边界值需要考虑！！！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

    // 第二想法，边中序遍历边判断
    // int pre = INT_MIN; 先弄一个初始值,但如果这样初始化,会出现INT_MIN边界值,导致结果为false!!!
long pre = (long)INT_MIN - 1;
bool flag = true;
bool isValidBST(TreeNode* root){
    InOrder(root);
    return flag;
}
void InOrder(TreeNode* root){
    if (root && flag){
        InOrder(root->left);
        if (pre >= root->val) flag = false;
        pre = root->val;
        InOrder(root->right);
    }
}

leetcode 99*. 恢复二叉搜索树

二叉搜索树中的两个节点被错误地交换。请在不改变其结构的情况下，恢复这棵树。

示例1：

输入: [1,3,null,null,2]

1
/
3
\
2

输出: [3,1,null,null,2]

3
/
1
\
2

感觉我有点被这个“困难”题给吓到了，所以并没有去思考思路。但是看了别人的答案后，发现其实是一道很简单的题。（事实证明，还是不懂）贴代码吧。。。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
TreeNode *t1, *t2, *pre; //记得每个都要加星号！
void recoverTree(TreeNode* root) {
    if (!root) return;
    inorder(root); 
    int temp = t1->val;
    t1->val = t2->val;
    t2->val = temp;
}
void inorder(TreeNode *root){
    if (!root) return;
    inorder(root->left);
    if (pre && pre->val > root->val){ // 要错误排序才交换
        // first swap occurence
        if (!t1) t1 = pre; 
        // 主要不明白的是这里，尽管这里记录的是第一次的逆序对。但是如果出现了两个逆序对，t1不更新，但是t2却可以更新。备注：现在懂了，题目规定了只有两个节点错误交换，一般是这种情况1,3,2,4或者1,4,3,2,5（只需交换4 2）
        t2 = root;
    }
    pre = root;
    inorder(root->right);
}

leetcode 100. 相同的树

按照最简单的思维去思考！不要想得太复杂！

1
2
3
4
5
6
bool isSameTree(TreeNode* p, TreeNode* q) {
    // 结构和节点值都要相同
    if (!p && !q) return 1;
    if ((!p && q) || (p && !q) || p->val != q->val) return 0;
    return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}

leetcode 101*.对称二叉树

给定一个二叉树，检查它是否是镜像对称的。

例如，二叉树 [1,2,2,3,4,4,3] 是对称的。

1
2
3
4
5
   1
   / \
  2   2
 / \ / \
3  4 4  3

但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:

1
2
3
4
5
  1
 / \
2   2
 \   \
 3    3

递归，多思考一下就能想出来：

1
2
3
4
5
6
7
8
9
bool isSymmetric(TreeNode* root) {
    if (!root) return 1;
    return judge(root->left, root->right);
}
bool judge(TreeNode* a, TreeNode* b){
    if (!a && !b) return 1;
    if ((!a && b) || (a && !b)) return 0;
    return (a->val == b->val) && judge(a->left, b->right) && judge(a->right, b->left);//只有在值相等的条件下，才比较其左右子树
}

坑爹的是，自己写了很久的迭代写法，但是一直都是错的。就是利用队列层次遍历的那种常规操作，写出来的结果一直不对。最后，只能参考官方教程的做法， 当然，这样做其实效率更高，空间也用的少。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
bool isSymmetric(TreeNode* root){
    if (!root) return 1;
    queue<TreeNode*> Q;
    Q.push(root);
    Q.push(root);
    while (!Q.empty()){
        TreeNode* t1 = Q.front();
        Q.pop();
        TreeNode* t2 = Q.front();
        Q.pop();
        // 此处与递归判断的时候不同，是continue，而不是返回True
        if (t1 == NULL && t2 == NULL) continue; 
        if (t1 == NULL || t2 == NULL) return 0;
        if (t1->val != t2->val) return 0;
        Q.push(t1->right);
        Q.push(t2->left);
        Q.push(t1->left);
        Q.push(t2->right);
    }
    return 1;
}

leetcode 102. 二叉树的层次遍历

给定一个二叉树，返回其按层次遍历的节点值。 （即逐层地，从左到右访问所有节点）。返回类型为vector>，即按层添加。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
vector<vector<int>> levelOrder(TreeNode* root) {
    vector<vector<int>> res;
    if (!root) return res;
    queue<TreeNode*> Q;
    TreeNode *t;
    Q.push(root);
    while (!Q.empty()){
        vector<int> temp;
        int len = Q.size();
        for (int i = 0; i < len; i++){ // 这里是按层添加的精髓。
            t = Q.front();
            if (t->left) Q.push(t->left);
            if (t->right) Q.push(t->right);
            temp.push_back(t->val);
            Q.pop();
        }
        res.push_back(temp);
    }
    return res;
}

leetcode 105*. 从前序与中序遍历序列构造二叉树

我之前在牛客做过，一直写的方法是利用构造多个vector序列。但是实际上这么写，空间和时间都有很大的复杂度！！！所以，今天看到了利用了hashmap的方法，特此记录。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
vector<int> preorder, inorder;
unordered_map<int, int> hashmap;
int preIndex = 0;
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
    this->preorder = preorder;
    this->inorder = inorder;
    int size1 = preorder.size(), size2 = inorder.size();
    if (size1 == 0 || size2 == 0 || size1 != size2) return 0;
    for (int i = 0; i < size1; i++){
        hashmap[inorder[i]] = i; // here!!!
    }
    return builder(0, size1 - 1);
}
TreeNode* builder(int mostleft, int mostright){
    if (mostleft > mostright) return NULL;
    int curval = preorder[preIndex];
    TreeNode* root = new TreeNode(curval);
    preIndex++;
    root->left = builder(mostleft, hashmap[curval] - 1); // 先构建左子树，因为先序遍历就是这样
    root->right = builder(hashmap[curval] + 1, mostright);
    return root;
}

leetcode 106*. 从中序与后序遍历序列构造二叉树

这一题与前一题基本类似，同样用hashmap来加快时间效率。然而！！！在创建左右子树的时候，应当先创建右子树，再创建左子树（因为后序遍历的尾巴就先是右子树），不然会出错！！！

而由前序和中序构造二叉树，则要先创建左子树，再创建右子树！！！

leetcode 108*. 将有序数组转换为二叉搜索树

转换后的二叉搜索树需要是高度平衡二叉树。没有思路，但是看了答案后发现其实很简单。从有序数组的中间部分划分左右子树，就可以确保二叉搜索树是高度平衡的了！！要注意一点，中间部分对于偶数长度的数组来说，可能选左边的，也可能选右边的，所以答案的结果不唯一。

1
2
3
4
5
6
7
8
9
10
11
12
TreeNode* sortedArrayToBST(vector<int>& nums) {
    if (nums.size() == 0) return NULL;
    return BuildTree(nums, 0, nums.size() - 1);
}
TreeNode* BuildTree(vector<int>& nums, int i, int j){
    if (i > j) return NULL;
    int mid = i + (j - i) / 2; 
    TreeNode* root = new TreeNode(nums[mid]);
    root->left = BuildTree(nums, i, mid - 1);
    root->right = BuildTree(nums, mid + 1, j);
    return root;
}

leetcode 110*. 平衡二叉树

判断是否为平衡二叉树。我一开始是跟着自己在牛客网写的代码那样的写法来写，但是始终过不了leetcode的样例。后来，真相大白，我的代码确实有错误！！这也说明，牛客的样例和leetcode的样例相比不够全。

1
2
3
4
5
6
7
8
9
10
11
12
13
bool isBalanced(TreeNode* root) {
    if (!root) return 1;
    int left = getHeight(root->left);
    int right = getHeight(root->right); 
    // 注释这么写就是没有继续递归判断，相当于只计算了根节点的左右两个子树是否平衡，但没有判断余下的子树！！
    // return abs(left - right) > 1 ? 0 : 1;
    if (abs(left - right) > 1) return 0;
    return isBalanced(root->left) && isBalanced(root->right);
}
int getHeight(TreeNode* root){
    if (!root) return 0;
    return max(getHeight(root->left), getHeight(root->right)) + 1; // 要继续判断接下来的子树
}

leetcode 109*. 有序链表转换二叉搜索树

这道题和108题有点类似，区别是输入不再是数组，而是一个升序链表。我一开始是将链表中的元素取出来放到数组中，再按照108题做，然而，运行效率和空间复杂度太高了！

实际上，我们可以按照那道题的思想，找出链表里中点的位置，再进行指针的转换。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
TreeNode* sortedListToBST(ListNode* head){
    if (!head) return NULL;
    if (!head->next) return new TreeNode(head->val);
    ListNode* pre = head, *slow = head->next, *fast = head->next->next;
    while (fast && fast->next){
        pre = pre->next;
        slow = slow->next;
        fast = fast->next->next; 
    } // slow抵达中点
    pre->next = NULL;
    TreeNode* root = new TreeNode(slow->val);
    root->left = sortedListToBST(head);
    root->right = sortedListToBST(slow->next);
    return root;
}

leetcode 222

求完全二叉树的节点个数。

1
2
3
4
int countNodes(TreeNode* root) {
    if (!root) return 0;
    return countNodes(root->left) + countNodes(root->right) + 1;
}

leetcode 72. 编辑距离

给定两个单词 word1 和 word2，计算出将 word1 转换成 word2 所使用的最少操作数 。

你可以对一个单词进行如下三种操作：

  1. 插入一个字符
  2. 删除一个字符
  3. 替换一个字符

示例 1:

输入: word1 = “horse”, word2 = “ros”
输出: 3
解释:
horse -> rorse (将 ‘h’ 替换为 ‘r’)
rorse -> rose (删除 ‘r’)
rose -> ros (删除 ‘e’)

示例 2:

输入: word1 = “intention”, word2 = “execution”
输出: 5
解释:
intention -> inention (删除 ‘t’)
inention -> enention (将 ‘i’ 替换为 ‘e’)
enention -> exention (将 ‘n’ 替换为 ‘x’)
exention -> exection (将 ‘n’ 替换为 ‘c’)
exection -> execution (插入 ‘u’)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
int minEditDistance(string word1, string word2) {
    if (word1.size() == 0 && word2.size() == 0) return 0;
    int m = word1.size(), n = word2.size();
    vector<vector<int>> cost(m + 1, vector<int>(n + 1, 0));
    for (int i = 0; i < n + 1; i++) {
        cost[0][i] = i;
    }
    for (int i = 0; i < m + 1; i++) {
        cost[i][0] = i;
    }
    for (int i = 1; i <= m; i++) {
        for (int j = 1; j <= n; j++) {
            if (word1[i - 1] == word2[j - 1]) { // 相等，无需变动
                cost[i][j] = cost[i - 1][j - 1]; 
            }
            else {
                // cost[i-1][j-1]:替换操作
                // cost[i-1][j]:删除
                // cost[i][j-1]:插入
                cost[i][j] = min(min(cost[i - 1][j - 1], cost[i - 1][j]), cost[i][j - 1]) + 1;
            }
        }
    }
    return cost[m][n];
}

数学

leetcode 29. 两数相除

给定两个整数，被除数 dividend 和除数 divisor。将两数相除，要求不使用乘法、除法和 mod 运算符。返回被除数 dividend 除以除数 divisor 得到的商。

思路：很不擅长这类限制使用运算符的题目。参考他人的写法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
int divide(int dividend, int divisor) {
    // 边界条件要全面解决！
    if (dividend == 0) return 0;
    if (dividend == INT_MIN && divisor == -1) return INT_MAX; 
    if (dividend == INT_MIN && divisor == 1) return INT_MIN;
    bool flag = 1; // 判断结果的正负号
    if ((dividend > 0 && divisor < 0) || (dividend < 0 && divisor > 0)){
        flag = 0;
    } 
    long t = abs((long) dividend); // 用int会溢出，所以用long
    long d = abs((long) divisor);
    int res = 0;
    for (int i = 31; i >= 0; i--){ // 左移是乘2，右移是除以2
        if ((t >> i) >= d){ // 此部分是关键，要自己体会
            t -= d << i;
            res += 1 << i;
        }
    }
    return flag > 0 ? res : -res;
}

633. 平方数之和

给定一个非负整数 c ，你要判断是否存在两个整数 a 和 b，使得 a2 + b2 = c。

用滑动窗口来做。但是，这道题有点坑，主要是在int类型上可能会超，因此要自己学会判断。

1
2
3
4
5
6
7
8
9
10
11
12
bool judgeSquareSum(int c){
    int end = sqrt(c);
    int start = 0;
    while (start <= end){
        if (start * start == c - end * end) return true;
        else if (start * start < c - end * end){
            start++;
        }
        else end--;
    }
    return false;
}

排序

面试题10.01. 合并排序的数组

给定两个排序后的数组 A 和 B，其中 A 的末端有足够的缓冲空间容纳 B。 编写一个方法，将 B 合并入 A 并排序。

初始化 A 和 B 的元素数量分别为 m 和 n。

示例:

1
2
3
4
5
输入:
A = [1,2,3,0,0,0], m = 3
B = [2,5,6],       n = 3

输出: [1,2,2,3,5,6]

我被自己愚蠢到了。一直想着，把A数组中的数字先往后挪，再利用归并排序从头开始填入数字，然而，这样做在挪数字时会出现很多的错误。其实，从A数组末尾开始比较着填数字就好了，是我太傻了。

1
2
3
4
5
6
7
8
9
10
11
void merge(vector<int>& A, int m, vector<int>& B, int n) {
    // 想复杂了。。。从尾部开始填充数据就好了，唉。
    int index = m + n - 1;
    m--; n--;
    while (m >= 0 || n >= 0){
        if (m < 0 || (n >= 0 && B[n] >= A[m])){
            A[index--] = B[n--];
        }
        else A[index--] = A[m--];
    }
}

BFS

BFS通常用来求解最短路径问题。要学会“抽象”问题。

leetcode 127. 单词接龙

给定两个单词（beginWord 和 endWord）和一个字典，找到从 beginWord 到 endWord 的最短转换序列的长度。转换需遵循如下规则：每次转换只能改变一个字母， 转换过程中的中间单词必须是字典中的单词。

说明: 如果不存在这样的转换序列，返回 0； 所有单词具有相同的长度 ；所有单词只由小写字母组成 ；字典中不存在重复的单词。你可以假设 beginWord 和 endWord 是非空的，且二者不相同。
示例 1:

输入:
beginWord = “hit”,
endWord = “cog”,
wordList = [“hot”,”dot”,”dog”,”lot”,”log”,”cog”]

输出: 5

解释: 一个最短转换序列是 “hit” -> “hot” -> “dot” -> “dog” -> “cog”,
返回它的长度 5。

思路：这一题就是需要有抽象思维。每个单词是一个结点，只有相差一个字符的点之间才有路径，路径权值全部为1. 本质就是求图的两点最短路径问题！！！因此，用BFS来做最为合适。

leetcode 994*. 腐烂的橘子

在给定的网格中，每个单元格可以有以下三个值之一：

值 0 代表空单元格；
值 1 代表新鲜橘子；
值 2 代表腐烂的橘子。
每分钟，任何与腐烂的橘子（在 4 个正方向上）相邻的新鲜橘子都会腐烂。

返回直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能，返回 -1。

img

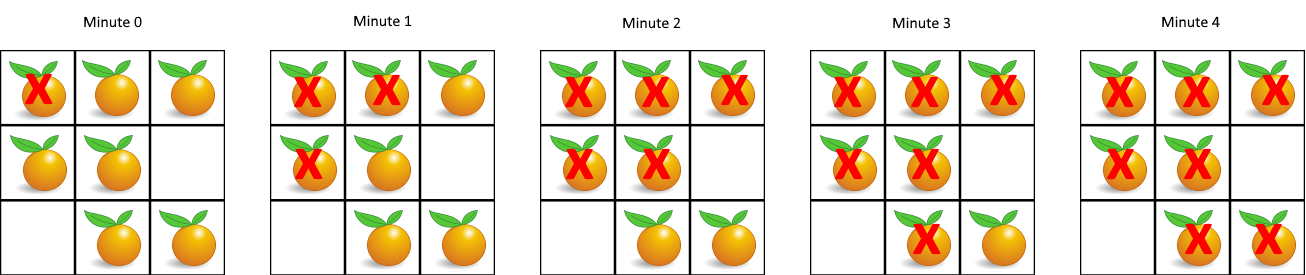
思路：这道题应该用广度优先遍历（虽然我一开始没有看出来）。这里类似于树的广度遍历：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
int orangesRotting(vector<vector<int>>& grid) {
    int n = grid.size(), m = grid[0].size();
    int res = 0;
    int dir_x[4] = {0, 1, -1, 0};
    int dir_y[4] = {1, 0, 0, -1};
    queue<pair<int, int>> Q;
    for (int i = 0; i < n; i++){ //将腐烂橘子压入队列
        for (int j = 0; j < m; j++){
            if (grid[i][j] == 2) Q.push({i, j});
        }
    }
    while (!Q.empty()){
        int vol = Q.size(); //标记队列内腐烂橘子个数,这里的做法和树的广度遍历很像！
        for (int i = 0; i < vol; i++){
            pair<int, int> x = Q.front();
            Q.pop();
            for (int i = 0; i < 4; i++){
                int tx = x.first + dir_x[i];
                int ty = x.second + dir_y[i];
                if (tx >= 0 && tx < n && ty >= 0 && ty < m && grid[tx][ty] == 1){ //判断是否存在新鲜橘子
                    grid[tx][ty] = 2;
                    Q.push({tx, ty});
                }
            }
        }
        if (!Q.empty()){ //如果为空表示一开始就没有腐烂橘子，返回0分钟
            res++;  //每次取出队列所有橘子时间加1，同时压入被污染的新一批橘子
        }
    }
    for (int i = 0; i < n; i++){
        for(int j = 0; j < m; j++){
            if (grid[i][j] == 1) return -1;
        }
    }
    return res;
}

111. 二叉树的最小深度

用BFS来求。一旦遍历到左右子树均为空的结点，则返回当前深度。

也可以递归来做：

1
2
3
4
5
6
int minDepth(TreeNode* root){
    int left = minDepth(root->left), right = minDepth(root->right);
    return (left && right) ? 1 + min(left, right) : 1 + left + right
    // 之所以后面是1+left+right,这个时候left或者right一定有一个是0
    // 这样加上一个0，对另一个变量的值不会有影响，如果另一个是0 那就返回0+0+1否则返回另一个不为0的变量的值+1
}

DFS

leetcode 200. 岛屿数量

给定一个由 ‘1’（陆地）和 ‘0’（水）组成的的二维网格，计算岛屿的数量。一个岛被水包围，并且它是通过水平方向或垂直方向上相邻的陆地连接而成的。你可以假设网格的四个边均被水包围。

示例 1:

1
2
3
4
5
6
7
输入:
11110
11010
11000
00000

输出: 1

标准DFS，但是很多细节要注意啊！！！另外，可以不用辅助数组就不用！！！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Solution {
public:
    int numIslands(vector<vector<char>>& grid) {
        if (grid.size() == 0) return 0;
        int m = grid.size(), n = grid[0].size();
        // vector<vector<bool>> visited(m, vector<bool>(n, 0));
        // memset(visited, 0, sizeof(visited));
        int cnt = 0;
        for (int i = 0; i < m; i++){
            for (int j = 0; j < n; j++){
                if (grid[i][j] == '1'){
                    // dfs(grid, visited, i, j);
                    dfs2(grid, i, j);
                    cnt++;
                }
            }
        }
        return cnt;
    }

    void dfs2(vector<vector<char>>& grid, int i, int j){ // 无需使用辅助数组
        if (i < 0 || i >= grid.size() || j < 0 || j >= grid[0].size() || grid[i][j] != '1'){
            return;
        }
        grid[i][j] = '2';
        dfs2(grid, i + 1, j);
        dfs2(grid, i - 1, j);
        dfs2(grid, i, j + 1);
        dfs2(grid, i, j - 1);
    }

    void dfs(vector<vector<char>>& grid, vector<vector<bool>>& visited, int i, int j){
        if (i < 0 || i >= grid.size() || j < 0 || j >= grid[0].size() || visited[i][j] || grid[i][j] == '0'){
            return;
        }
        visited[i][j] = 1;
        dfs(grid, visited, i + 1, j);
        dfs(grid, visited, i - 1, j);
        dfs(grid, visited, i, j - 1);
        dfs(grid, visited, i, j + 1);
    }
};

leetcode 130. 被围绕的区域

给定一个二维的矩阵，包含 'X' 和 'O'（字母 O）。

找到所有被 'X' 围绕的区域，并将这些区域里所有的 'O' 用 'X' 填充。

1
2
3
4
X X X X
X O O X
X X O X
X O X X

运行后变为：

1
2
3
4
X X X X
X X X X
X X X X
X O X X

思路：其实，这道题要学会换个思路。我们不应该一直想着怎么求出被‘X’围绕的区域，而是可以从边界上的’O’来下手，这样就可以用普通的BFS或者DFS方法来做了！这里就不贴代码了，用DFS来做比较简单。

贪心

leetcode 452. 用最少数量的箭引爆气球

在二维空间中有许多球形的气球。对于每个气球，提供的输入是水平方向上，气球直径的开始和结束坐标。由于它是水平的，所以y坐标并不重要，因此只要知道开始和结束的x坐标就足够了。开始坐标总是小于结束坐标。平面内最多存在104个气球。

一支弓箭可以沿着x轴从不同点完全垂直地射出。在坐标x处射出一支箭，若有一个气球的直径的开始和结束坐标为 xstart，xend， 且满足 xstart ≤ x ≤ xend，则该气球会被引爆。可以射出的弓箭的数量没有限制。 弓箭一旦被射出之后，可以无限地前进。我们想找到使得所有气球全部被引爆，所需的弓箭的最小数量。

Example:

1
2
3
4
5
6
7
8
输入:
[[10,16], [2,8], [1,6], [7,12]]

输出:
2

解释:
对于该样例，我们可以在x = 6（射爆[2,8],[1,6]两个气球）和 x = 11（射爆另外两个气球）。

思路：贪心思想。先按照气球的x_end坐标由小到大排序。然后再查看接下来气球的x_start是否大于这个first_end.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int findMinArrowShots(vector<vector<int>>& points) {
    if (points.size() == 0) return 0; //边界条件不能忘！
    // 贪心法
    sort(points.begin(), points.end(), cmp); // 根据x_end将气球进行排序
    int first_end = points[0][1]; 
    int arrows = 1;
    for (int i = 1; i < points.size(); i++){
        if (points[i][0] > first_end){ // 大于first_end，说明不可以同时引爆
            arrows += 1;
            first_end = points[i][1];
        }
    }
    return arrows;
}

static bool cmp(vector<int> a, vector<int> b){
    return a[1] < b[1];
}

其他

leetcode 54. 螺旋矩阵

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
vector<int> spiralOrder(vector<vector<int>>& matrix) {
    vector<int> res;
    if (matrix.empty()) return res;
    int m = matrix.size(), n = matrix[0].size();
    int up = 0, down = m - 1, left = 0, right = n - 1;
    while (true){
        for (int i = left; i <= right; i++) res.push_back(matrix[up][i]);
        if (++up > down) break;
        for (int i = up; i <= down; i++) res.push_back(matrix[i][right]);
        if (--right < left) break;
        for (int i = right; i >= left; i--) res.push_back(matrix[down][i]);
        if (--down < up) break;
        for (int i = down; i >= up; i--) res.push_back(matrix[i][left]);
        if (++left > right) break;
    }
    return res;

额外找：

5 一个数组a，判断是否存在i<j<k, a[i]<a[k]<a[j]（撕代码）

6 找到一个字符串中不重复子串的最大长度（撕代码）

7 一个二叉搜索树，找出小于m的最大数（撕代码）

算法题：两个有序数组求交集

给定一个表，列名如下，

user | video | time

查询每个用户第二个看得视频，请写出sql语句。

作者：Johnny想要offer
https://www.nowcoder.com/discuss/199615来源：牛客网

一道基于抖音的sql题目：

给定一个表，列名如下，

user | video | time

查询每个用户第二个看得视频，请写出sql语句。

写出统计用户数量的sql语句。

2 交叉熵损失函数公式怎么写

3 最大似然估计公式

4 梯度爆炸lstm怎么解决

5 一个数组a，判断是否存在i<j<k, a[i]<a[k]<a[j]（撕代码）

6 找到一个字符串中不重复子串的最大长度（撕代码）

7 一个二叉搜索树，找出小于m的最大数（撕代码）

8 linux找上一个使用命令

9 vim定位到第一行

千万向量中找到和单个向量相似的那个，先聚类，再然后输入向量先与聚类中心比较再与类中的向量比较。

模型为了拟合数据而调节参数改变模型形状，正则则是使得模型形状更为平缓，使得泛化能力增加，而bias则只会使得模型平移，因此正则bias应该没什么效果

transformer结构

既然LR解决的是分类问题，它为什么叫逻辑回归

https://www.jianshu.com/p/3956c2eb070e

https://blog.csdn.net/qq_38358305/article/details/88242839